

Video Message by Professor Salim Al-Hassani to the“Science and Technology in Islamic Civilization” conference
by Media Desk

The complex of disciplines composed of mathematics, architecture and art in Islamic civilisation has been an important field of recent research. The scholars showed the interaction between mathematical reflexion and procedures and their implementation in designing concrete and symbolic forms in buildings, decoration and design. Furthermore, recent scholarship pointed out the amazing progress that this marriage brought about in prefiguring outstanding mathematical results that scientists proved only in late 20th century. In the following survey, Professor Salim Al-Hassani explores the various facets of this exciting subject that is still full of discoveries to come. By drawing attention to the ongoing debates in scholarly circles among physicicts, mathematicians and historians of science, art and architecture, he shows how the connection between theoretical and applied mathematics was fruitful and creative in the Islamic tradition


Note of the editor
This essay is a revised and expanded version of a lecture presented at the 28th Annual Conference on the History of Arabic Sciences organised by the Institute for the History of Arabic Sciences, Aleppo University, Aleppo, Syria, in 25-27 April 2007. It was submitted for publication in the proceedings of the conference.
***
Table of contents
1. Introduction
2. Geometry at the basis of Islamic architectural decoration
3. The ‘Muqarnas’ Project
4. Conflicting Views on Mathematical Islamic Art
4.1. Dr Zohor Idrisi’s View
4.2. Professor George Saliba’s View
5. The Work of Alpay Özdural
6. Combination of Mathematics, Astronomy, Art and Architecture
7. Conclusion
8. Bibliography and Resources
***
“Sophisticated geometry in Islamic architecture”, “Geometry meets artistry in medieval tile work”, “Geometry meets Arts in Islamic tiles”. These were some of the headlines we saw in February 2007 in the main news agencies and science dispatches giving coverage to an exciting discovery published by two American scholars, Peter J. Lu and Paul J. Steinhardt (respectively from the Department of Physics at Princeton and Harvard universities).[1] The discovery is “that medieval Islamic artists produced intricate decorative patterns using geometrical techniques that were not understood by Western mathematics until the second half of the 20th century”. The combinations of ornate stars and polygons that have adorned mosques and palaces since the 15th century were created using a set of just five template tiles, which could generate patterns with a kind of symmetry that eluded formal mathematical description for another 500 years. The authors suggest that the Islamic artisans who created these typical girih[2] designs had an intuitive understanding of highly complex mathematical concepts. They also suggest that these could be proof of a major role of mathematics in medieval Islamic art or it could have been just a way for artisans to construct their art more easily.
Girih designs feature arrays of tessellating polygons of multiple shapes, and are often overlaid with a zigzag network of lines. It had been assumed that straightedge rulers and compasses were used to create them — an exceptionally difficult process as each shape must be precisely drawn. From the 15th century, however, some of these designs are symmetrical in a way known today as “quasi-crystalline”. Such forms have either fivefold or tenfold rotational symmetry — meaning they can be rotated to either five or ten positions that look the same — and their patterns can be infinitely extended without repetition. The principles behind quasi-crystalline symmetry were calculated by the Oxford mathematician Roger Penrose in the 1970s, but it is now clear that Islamic artists were creating them more than five centuries earlier.
The present paper reviews this discovery and discusses related literature on the subject of mathematics and arts in Muslim heritage. In particular, it accounts the related works of:
1. Alpay Özdural who showed how such geometrical patterns were used to solve cubic algebraic equations and also used the manuscript of Abu’l-Wafa and other mathematical Islamic mathematical treatises as evidence that mathematicians instructed artisans,
2. Gülru Necipoglu who discussed geometry, muqarnas and the contribution of the mathematical sciences and
3. George Saliba who presented critical arguments against some of the derived conclusions.
4. Zohor Idrisi who belives that ongoing work on Islamic tiles lacks the essential historical context that is required to inform the reader of how and when these mathematical techniques developed.
It is hoped that this review paper will bring to life the debate on the subject of Mathematics and Islamic Art and Architecture.
2. Geometry at the basis of Islamic architectural decoration
A study of medieval Islamic art has shown that some of its geometric patterns use principles established only centuries later by modern mathematicians. In particular, recent research has provided the ground for the astonishing claim that 15th century Muslim architects and artists used techniques inspired by what mathematicians nowadays call “quasicrystalline geometry”. This indicates intuitive understanding of complex mathematical formulae, even if the artisans had not worked out the underlying theory.


Figure 1: A computer reconstruction of the quasicrystalline patterns of the Darb-i Imam shrine (Isfahan, Iran), which was built in 1453 (Science Magazine, vol. 315, n° 1106, 2007).
The discovery was published in the journal Science in February 2007 by Paul J. Steinhardt and Peter J. Lu.[3] The research shows that an important breakthrough had occurred in Islamic mathematics and design by 1200. The core of the discovery claims that Muslim architects of central Asia made tilings that reflected mathematics, they were so sophisticated that they were only figured out in the last decades of our age.
The similarity between ancient Islamic designs and contemporary quasicrystalline geometry lies in the fact that both use symmetrical polygonal shapes to create patterns that can be extended indefinitely. Until now, the conventional view was that the complicated star-and-polygon patterns of Islamic design were conceived as zigzagging lines drafted using straightedge rulers and compasses.
With this discovery, one can conclude that the combinations of ornate stars and polygons that have adorned mosques and palaces since the 15th century were created using a set of just five template tiles, which could generate patterns with a kind of symmetry that eluded formal mathematical description for another 500 years.
The discovery suggests that the Islamic artisans who created these typical girih designs had an intuitive understanding of highly complex mathematical concepts. “We can’t say for sure what it means,” says Lu, a graduate student in physics at Harvard’s Graduate School of Arts and Sciences. “It could be proof of a major role of mathematics in medieval Islamic art or it could have been just a way for artisans to construct their art more easily. It would be incredible if it were all coincidence, though. At the very least, it shows us a culture that we often don’t credit enough was far more advanced than we ever thought before.” [4]




Figure 2A & 2B: Girih tile reconstruction of the strapwork pattern on an interior archway in the Sultan’s Lodge in the Green Mosque in Bursa, Turkey. Adapted from Science Magazine, vol. 315, n° 1106, 2007) and Hamish Johnston, “Islamic quasicrystals’ predate Penrose tiles“, Physicsworld.com, Feb 22, 2007
Girih designs feature arrays of tessellating polygons of multiple shapes, and are often overlaid with a zigzag network of lines. It had been assumed that straightedge rulers and compasses were used to create them — an exceptionally difficult process as each shape must be precisely drawn. From the 15th century, however, some of these designs are symmetrical in a way known today as “quasi-crystalline”. Such forms have either fivefold or tenfold rotational symmetry — meaning they can be rotated to either five or ten positions that look the same — and their patterns can be infinitely extended without repetition. The principles behind quasi-crystalline symmetry were calculated by the Oxford mathematician Roger Penrose in the 1970s, but it is now clear that Islamic artists were creating them more than 500 years earlier.
Peter Lu, one of the authors of this discovery, began wondering whether there were quasi-crystalline forms in Islamic art after seeing decagonal artworks in Uzbekistan, while he was there for professional reasons. On returning to Harvard, he started searching the university’s vast library of Islamic art for quasi-crystalline designs. He found several, as well as architectural scrolls that contained the outlines of five polygon templates — a ten-sided decagon, a hexagon, a pentagon, a rhombus and a bow-tie shape — that can be combined and overlaid to create such patterns.
In keeping with the Islamic tradition of not depicting images of people or animals, many religious buildings were decorated with geometric star-and-polygon patterns, often overlaid with a zigzag network of lines. Lu and Steinhardt show in their study published in the journal Science that by the 13th century Islamic artisans had begun producing patterns using a small set of decorated, polygonal tiles which they call “girih” tiles.


Figure 3: Periodicgirih pattern from the Seljuk Mama Hatun Mausoleum in Tercan, Turkey (~1200 CE), with girih-tile reconstruction overlaid at bottom.
Art historians have until now assumed that the intricate tile work had been created using straight edges and compasses, but the study suggests that Muslim artisans were using a basic toolkit of girih tiles made up of shapes such as the decagon, pentagon, diamond and hexagon.
“Straight edges and compasses work fine for the recurring symmetries of the simplest patterns we see, but it probably required far more powerful tools to fully explain the elaborate tiling with decagonal [10-sided] symmetry,” P. J. Lu said, quoted by the journal The Independent on 25 February 2007. He adds that “individually placing and drafting hundreds of decagons with a straight edge would have been exceedingly cumbersome. It’s more likely these artisans used particular tiles that we’ve found by decomposing the artwork”.[5]
The scientists found that by 1453, Islamic architects had created overlapping patterns with girih tiles at two sites to produce near-perfect quasi-crystalline patterns that did not repeat themselves. “The fact that we can explain so many sets of tiling, from such a wide range of architectural structures throughout the Islamic world with the same set of tiles, makes this an incredibly interesting universal picture,” P. J. Lu said.[6]
With this result, despite the debate that surrounded it in scholarly circles, we can see that very important discoveries in the Islamic scientific tradition are still to come, and that with the continuing research in different sources, including those of material remains of Muslim civilisation, the picture of our knowledge may be enriched and even changed dramatically.
As a background to the present day research on Islamic architecture as a conjunction of mathematics, arts and practical knowledge, we can mention the ongoing work on the Muqarnas. A Muqarnas is a type of corbel used as a decorative device in traditional Islamic architecture. The term is the Arabic word for stalactite vault, an architectural ornament developed around the middle of the 10th century in north eastern Iran and almost simultaneously, but apparently independently, in central North Africa. A Muqarnas is a three-dimensional architectural decoration composed of niche like elements arranged in tiers. The two-dimensional projection of a Muqarnas vault consists of a small variety of simple geometrical elements. Excellent examples can be found in the Alhambra in Granada, and in the mausoleum of Sultan Qaitbay in Cairo.[7]


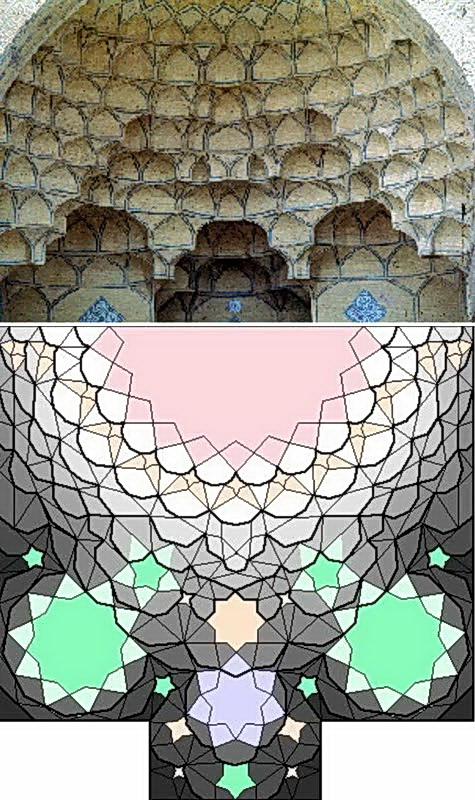

Figures 4: The iwans that surround the courtyard of Masjid-i-Jame in Isfahan consist of three Muqarnas, each giving different impressions: (4A) the southern Muqarnas, occupying a frontal position facing the courtyard, has an apex made up of 8 segments, suggesting a primitive strength; (4B)the eastern Muqarnas, with its 11-segmented apex, is complex and not aesthetically pleasing.


(4C) the western Muqarnas has a 5-segment apex, and displays an elegant form such as that seen in Hakuho sculptures.(Source).
The singular beauty of the Muqarnas has been reported by travellers throughout history. Their descriptions, however, are no more than brief introductions, and many details remain unclear. In his work on such architectural ornaments, Shiro Takahashi created exact drawings of many varieties of Muqarnas, classifying them into types in an attempt to clarify the formative styles of Muqarnas.[8]
On the other hand, scholars from Heidelberg University in Germany, led by Yvonne Dold-Samplonius, designed The Muqaras Project aimed at the study of Muqarnas tradition in Islamic architecture. The project is entitled: Mathematical Concepts and Computer Graphics for the Reconstruction of Stalactite Vaults – Muqarnas – in Islamic Architecture.[9]
The focus in this project is laid on two main points. One is that, from the late 11th century on, all Muslim lands adopted and developed the Muqarnas, which was widely used in constructions. The second and far more important point is that, from the moment of its first appearance, the Muqarnas acquired four characteristic attributes, whose evolution and characteristics form its history: it was three-dimensional and therefore provided volume wherever it was used, the nature and depth of the volume being left to the discretion of the maker; it could be used both as an architectonic form, because of its relationship to vaults, and as an applied ornament, because its depth could be controlled; it had no intrinsic limits, since not one of its elements is a finite unit of composition and there is no logical or mathematical limitation to the scale of any one composition; and it was a three-dimensional unit which could be resolved into a two-dimensional outline.
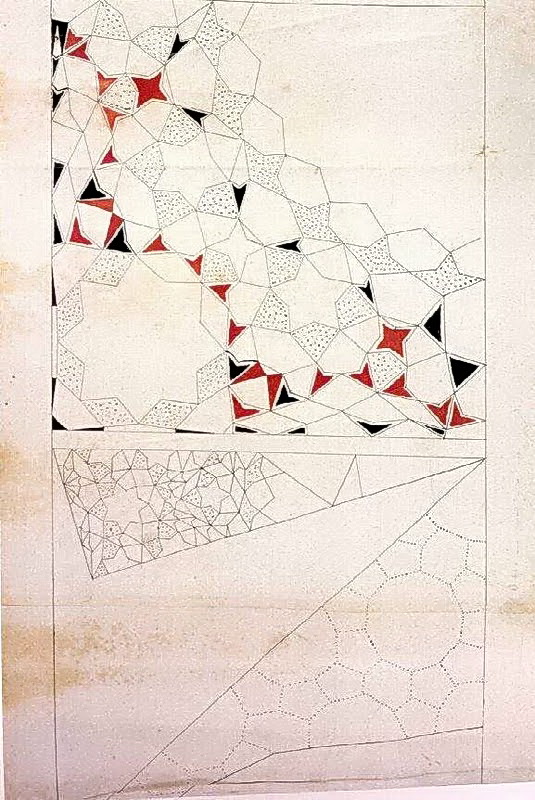



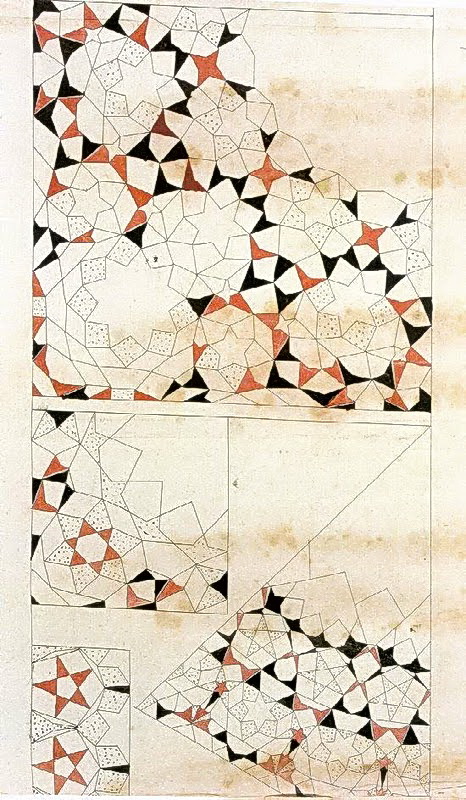

Figures 5: Muqarnas drawings in The Topkapi Scroll, the best preserved example of its kind, displaying geometry and ornament of Islamic architecture: (5A) Vault fragment with black-dotted polygonal grid lines, triangular one-twentieth repeat unit of a decagonal vault, and fan-shaped radial Muqarnas quarter vault; (5B) Fan-shaped radial muqarnas quarter vault, and shell-shaped radial muqarnas quarter vault; (5C) Fan-shaped radial muqarnas quarter vault, rhombodial one-eight repeat unit of an octagonal fan-shaped radial muqarnas quarter vault, fan-shaped radial muqarnas quarter vault, and rectangular repeat unit of stellate Muqarnas fragment. (Source).
“The muqarnas is a ceiling like a staircase with facets and a flat roof. Every facet intersects the adjacent one at either a right angle, or half a right angle, or their sum, or another combination of these two. The two facets can be thought of as standing on a plane parallel to the horizon. Above them is built either a flat surface, not parallel to the horizon, or two surfaces, either flat or curved, that constitute their roof. Both facets together with their roof are called one cell. Adjacent cells, which have their bases on one and the same surface parallel to the horizon, are called one tier.” [10]The work of the group is based on the analysis made by Yvonne Dold-Samplonius of the mathematical work of the 15th century Timurid mathematician Ghiyath al-Din Mas’ud al-Kashi (ca. 1380-1429). Al-Kashi defines the Muqarnas as:
Building on the classification of different varieties of Muqarnas by al-Kashi, the project analyses the intermediate elements which connect the roofs of adjacent cells. In this sense, al-Kashi distinguishes four types of Muqarnas: The Simple Muqarnas and the Clay-plastered Muqarnas, both with plane facets and roofs, as well as the Curved Muqarnas, or Arch, and the Shirazi, in which the roofs of the cells and the intermediate elements are curved. The plane projection of a simple element (either cell or intermediate element) is a basic geometrical form , namely a square, half-square (cut along the diagonal), rhombus, half-rhombus (isosceles triangle with as base the shorter diagonal of the rhombus), almond (deltoid), jug (quarter octagon), and large biped (complement to a jug), and small biped (complement to an almond). Also rectangles occur.
The elements are constructed according to the same unit of measure, so they fit together in a wide variety of combinations. Al-Kashi uses in his computation the module of the Muqarnas, defined as the base of the largest facet (the side of the square) as a basis for all proportions.
The Muqarnas is used in large domes, in smaller cupola, in niches, on arches, and as an almost flat decorative frieze. In each instance the module as well as the depth of the composition is different and adapts to the size of the area involved or to the required purpose. The Muqarnas is at the same time a linear system and an organization of masses.[11]






Figures 6: South octagon vault of the Takht-i Suleyman (Throne of Salomon), the ruins of which are situated ca. 30 km North of Takab, N.W. of Tehran. Takht-i Suleyman was a palace built in the 13th century by the Ilkhanid ruler Abaqa (1265-1281). In the ruins of the western part of the palace a plate has been found, which was recognized as a construction plan for a Muqarnas vault. In analogy to this plan, the scholars of The Muqarnas Project at Heidelberg University in Germany proposed a possible plan to reconstruct the much simpler south octagon vault. (Source).
Departing from the existence of a lot of ground plans of existing Muqarnas, some of these 3D-vaults are still in good shape, others broke down and have to be reconstructed from their plans; but even in many cases such plans do not exist any more. The Muqarnas Project mentioned above intends to convert existing Muqarnas plans into the computer in such a way that their properties can be analyzed (what kind of elements occur, which elements can be connected and how, what are the possible heights of the succeeding tiers, what about regional differences, cultural differences, differences in time, and so forth). In addition, the inherent aim to such an investigation is to build a computer program that is able to answer these questions on Muqarnas plans automatically. The obvious material to start with, according to the scholars of this project, are the Illkhanid Muqarnas plans.[12] These plans can be compared with existing architecture and thus show limitations in computer possibilities.
In the second stage, the scholars are inclined to apply these methods on plans which are not known to have been realized, such as those recorded in the Topkapi Scroll. With all this knowledge in hand, it will be possible to apply these methods for different purposes, such as reconstructing Muqarnas vaults in ruins (like for instance in Varamin, Iran), or to produce short videos tapes on Muqarnas to be used for teaching.[13]
4. Conflicting Views on Mathematical Islamic Art
The subject of the influence of mathematicians on the artisans is a hotly debated subject which requires scholarly resolution. Recently, the author of this article consulted colleagues on this subject and in particular asked their views on the recent discoveries of Lu and Steinhardt. I give below the views of two contemporary scholars, Dr Zohor Idrisi and Prof. George Saliba. In addition, I account briefly of the tantalizing work achieved by the late Alpay Özdural.
Dr. Idrisi considers that we should not jump too quickly into claiming the ground breaking character of the ongoing work on tiling, tessellating and crystallography. This subject is far removed from Greek style elementary geometry. For mathematicians, the work on tiling is a real nightmare as it is a highly specialised field that industry has been researching ever since the 1970s with the work of Penrose.[14]
Scholars, such as Branko Grünbau[15] (from the University of Washington in Seattle), had worked intensively on the subject of tiling before P. J. Lu and P. J. Setinheardt published their article recently. Surprisingly though, Grünbaum’s work is coloured by the view point he expresses being that the Muslims did not understand the mathematics of their artistic work. It is interesting to note that several of the press reviews accounting of P. J. Lu and P. J. Setinheardt’s discovery are similar to those expressed by Grünbaum.
This is why Dr. Idrisi stresses that without doubt this discovery is a fascinating one for a mathematician, but the ongoing work on Islamic tiles lacks the essential historical context that is required to inform the reader of how and when these mathematical techniques developed.
4.2. Professor George Saliba’s View
Referring to the breakthrough the Harvard/Princeton scientists that already stormed the public media, Professor Saliba[16] wrote:
“I have seen several references to that, and of course in all instances the question of the relationship between the artisans and the mathematicians is brought up.
Thanks for looking into this relationship a little closer, and for finding out that I had already written something about it quite some time ago, and for referring to the article in which I discuss this relationship in Islamic civilization.[17] I hope this article is read carefully as it should constitute a good warning to those who jump to conclusions way too quickly. History does not work in that fashion, and I for one do not believe, nor can I defend a statement that says that artisans have achieved a breakthrough in the 15th century, or even earlier as some accounts now speculate, that bespoke of quasi-crystalline symmetries when the very concept of crystalline structures and their geometry was not known as far as I can tell. In my article… I warn that we should stick to the exhibitable evidence, preferably textual, before we jump to conclusions on how to interpret artistic designs, no matter how tempting the process of “discovering” breakthroughs is. The warning should be heeded especially when we are always accused of tooting our own horns way too loudly, and thus loosing credibility in the process. And that is why I stick to exhibitable evidence. Not speculation.
Of what I have read so far, the authors of the “discovery” of the breakthrough do not even claim that there was an exhibitable connection between the artisans’ work and the geometry of quasi-crystalline symmetries, and admit that they are speculating, and I agree with them that Islamic civilization never received its fair share of credit. But that does not mean that artisans achieved a breakthrough, the description that gets repeated in the press all over the place, when the very concept of the structures of crystalline symmetries had not even been conceived.
One of the participants in the discussion that I have read is a physicist down at Duke, and he even uses such terms as “almost” got it, but never says that the said symmetries were actually or precisely duplicated. I pay a much closer attention to this innocuous “almost”, just as much as Abu al-Wafa’ al-Buzjani did when he evaluated the artisans’ work of his time. They also “almost” got it.
I withhold comments on the subject until I find the textual evidence I argued for in my article.”
In the work of another scholar, the research on the Islamic complex of mathematics, architecture and art was conducted in another direction. Indeed, recently, Alpay Özdural, a scholar from the Eastern Mediterranean University in North Cyprus, carried on investigations the results of which he published in a series of articles.[18] Unfortunately, the early passing away on 22 February 2003 of this brilliant scholar has put an end to this wave of promising research.


Figure 7: Constructions 37 (left) and 42 (right) reconstructed by Alpay Özdural from the anonymous work On Interlocks of Similar or Corresponding Figures (Fi tadakhul al-ashkal al-mutashabiha aw al-mutawafiqa) (ca. 1300).
In one of his articles, Özdural draws conclusions from the analysis of two mathematical sources, On the Geometric Constructions Necessary for the Artisan (Kitab fima yahtaju ilayhi al-saani’ min al-a’mal al-handasiya) by Abu ‘l-Waf al-Buzjani (ca. 940-998), and an anonymous work, On Interlocks of Similar or Corresponding Figures (Fi tadakhul al-ashkal al-mutashabiha aw al-mutawafiqa) (ca. 1300).[19] These sources provide us with insight into the collaboration between mathematicians and artisans in the Islamic world. Studying this connection, the author presents a series of quotations from these two sources, which show that mathematicians taught geometry to artisans by means of cut-and-paste methods and of geometrical figures that had the potential of being used for ornamental purposes.


Figure 8: Decorative brickwork on the northern iwan of the Esfahan’s Great Mosque showing clockwise and counterclockwise swastikas in one of the circumferential bands. (Source).
Alpay Özdural points out in particular that the anonymous work on ornamental geometry, On interlocks of similar or complementary figures, appears to be compiled by a scribe at a series of meetings between mathematicians and artisans. Some of those constructions display the highest advancements attained by Muslim mathematicians thus represent the intimate link between theory and praxis that created the intriguing and awe-inspiring ornamental patterns. For instance, three of these are in fact the solutions to problems that require cubic equations. In those times mathematicians solved the cubic equations by means of conic sections; but such solutions were only for demonstration purposes with no practical application. These three constructions in Interlocks of Figures, which records the collaboration of mathematicians and artisans, are the cases of “moving geometry,” that is to say, mechanical procedures that are equivalent to the solutions for cubic equations.[20]
The first construction is about “a right-angled triangle such that if [a length equal to the shortest side] is cut from the hypotenuse of the triangle towards the shortest side and a perpendicular is erected at the point of cutting, it cuts off the intermediate side at a point where [the distance] from it to the right angle is equal to the perpendicular itself”. The solution is achieved by trial-and-error, i.e., by moving a straightedge around a pivotal point until the required position is reached. It actually corresponds to solving the cubic equationx³ + 2x² – 2x – 2 = 0 giving a real positive value of x=1.17 approximately.
The second construction concerns again the same right triangle; but in this case joining two such triangles facing opposite directions completes the rectangular repeat unit of the ornamental pattern in question. This time the moving instrument was a prototype of the T-square. It revolves around the centre of a circle so that the solution is achieved by the intersection of two implied hyperbolas, which is equivalent to equation x³ – 3x² – x + 1 = 0. The T-square, which appears to be introduced at that particular meeting, was meant to facilitate drawing patterns that involve conic sections. After the invention of this simple drafting instrument, we can interpret by hindsight that transmission of knowledge by way of architectural drawings-mostly ground plans based on square grids-gained impetus.
The third construction consists of four right-angled triangles rotating around a central square so as to form an ornamental pattern. The special property of this triangle is that “the altitude plus the shortest side is equal to the hypotenuse.” Omar Khayyam (1048-1122), the celebrated poet-mathematician, had written a treatise on this triangle and offered the solution of equation x³ – 20x² + 20x – 2000 = 0 by means of conic sections. The solution in Interlocks of Figures was achieved again with the aid of the T-square. In this case, its sliding movement translates the solution of equation x³ – 4x² + 6x – 2 = 0 into the intersection of a circle and a parabola, by way of focus-directrix property. The triangle that Omar Khayyam had discovered has other properties; it embodies what the Greeks called “the musical proportion.” A mathematical analysis of the North Dome Chamber (constructed in 1088-89 CE) of the Great Mosque of Isfahan, reveals that its proportions were generated wholly by Omar Khayyam’s triangle, thus exemplifying the active involvement of prominent mathematicians in the great accomplishments of Islamic architecture.
6. Combination of Mathematics, Astronomy, Art and Architecture
One recent discovery reveals that Muslim architects and scientists used mathematics far beyond producing decorative patterns. This is revealed in the Divrigi Ulu mosque, one of the masterpieces of Selçuk architecture located in Sivas, Turkey. It is known for its outstanding geometric styles and botanic designs. This astonishing mosque was founded in 1228 by the Mengücekid emir, Ahmet Shah. It was built by the architect Hürremsah from Ahlat. The UNESCO recognised, is cultural significance and it placed in the World Heritage List in 1985.
Recent discoveries show that there shadows of different silhouettes appear on the carvings of the outside walls of the mosque.During the different hours of a day, four shadows appear on the walls facing different directions: the first three are the silhouettes of a man looking straight, reading a book and praying, respectively, and the last one is the silhouette of a praying woman. These remarkable features could not have been designed without the combination of mathematics, astronomy and art. Actually, before the construction of the mosque had started, the scientists observed the positions of the sun and stars for two years. After very careful calculations had been done, the results were applied in the construction of the walls and the carving of the outside doors.




Figure 9: Divrigi Mosque praying man shadow.
In this short paper, our aim was to review some important results of the ongoing research on the connections of mathematics, architecture and art in Muslim heritage. It is obvious that this survey is far from covering the subject as it deserves. Our hope is that, by drawing the attention to these ongoing debates in scholarly circles, in particular Arab scholars, artists, mathematicians and architects will take a serious interest in this very exciting subject.
References
[1.] Peter J. Lu and Paul J. Steinhardt, “Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture,” Science vol. 315, n° 1106 (2007). See the review FSTC, A Discovery in Architecture: 15th-Century Islamic Architecture Presages 20th-Century Mathematics (published online on www.MuslimHeritage.com in 26 February, 2007) where numerous links to the article published in Science and to supporting online material, as well as links to media coverage resources for interested readers, are provided.
[2.] Girih as defined by Gülrun Necipoglu The Topkapi Scroll: Geometry and Ornament in Islamic Architecture:, Santa Monica, 1995, pp. 92-93): “The girih [is] a highly codified mode of geometric patterning with a distinctive repertoire of algebraically definable elements… The girih mode, with its two- and three-dimensional formulations compiled in surveying examples of pattern scrolls, is characterized by its self-consciously limited vocabulary of familiar, almost emblematic, star-and-polygon compositions generated by invisible grid systems that eliminated a broad spectrum of alternative geometric designs”.
[3.] Ibid
[4.] David Baron, “Medieval Islamic Architecture Presages 20th-Century Mathematics“, Harvard University Gazette, February 22, 2007.
[5.] Steve Connor, “Islamic artists were 500 years ahead of Western scientists”, The Independent (London), Friday, February 23, 2007.
[6.] Ibid
[7.] See on Muqarnas Doris Behrens-Abouseif, “Mukarnas”, Encyclopaedia of Islam, vol. VII, Leiden-New York: E.J.Brill, 1993; Naoko Fukami, “Studies on Muqarnas-vaulting in the Islamic Architecture: 1) the Area of central Asia: Khorasan, Khoarzum and Turan, Journal of the Society of Architectural Historians of Japan No. 22 (1994): pp. 2-36; Naoko Fukami, “Studies on Muqarnas-vaulting in the Islamic Architecture: 2) the Area of Iran: Mazandaran, Azerbaijan, Tehran, Isfahan and Yazd-Fars-kerman”, Journal of the society of Architectural Historians of Japan No. 25 (1996): pp. 23-61; Naoko Fukami, “Studies on Muqarnas-vaulting in the Islamic Architecture: 3) the Areas of Anatolia, Syria and Iraq”, Journal of the society of Architectural Historians of Japan No. 27 (1997): pp. 2-46; Kamil Haydar, Al-‘Amarah al-‘Arabiyya al-Islamiyyah: al-Khasa’is al-takhtitiyya li-‘l-muqarnasat [Arabic Islamic Architecture: Characteristics of Muqarnas], Beirut: Dar al-Fikr al-Lubnani, 1994. For a general bibliography and links, click here.
[8.] Shiro Takahashi, “Muqarnas: A Three-Dimentional Decoration of Islam Architecture“. See especially the “Muqarnas Database” comprising 617 ceiling plans and 1645 examples by Shiro Takahashi): for access, click here.
[9.] The group includes Silvia Harmsen, Susanne Krömker and Michael Winckler (Heidelberg University) and several international cooperation partners: Gülru Necipoglu Sackler (Museum Aga Khan Chair for the History of Architecture, Harvard), Mohammad Al-Assad (Center for the Study of the Built Environment, Amman), and Jan P. Hogendijk (Mathematical Institute, University of Utrecht): click here for more information. An important outcome of the research conducted by this group of scholars concerning al-Kashi’s contribution to architecture was issued as a video tape distributed by The American Mathematical Society: Qubba for al-Kâshî. Video Tape (Heidelberg: Institut für Wissenschaftliches Rechnen, Universität Heidelberg), 1996. Another video tape was produced later on by the same group: Yvonne Dold-Samplonius et al., Magic of Muqarnas: Stalactite Vaults in Islamic Architecture, Video, Duration 18 min, Format PAL or NTSC, May 2005.
[10.] Quoted in Yvonne Dold-Samplonius, “Practical Arabic Mathematics: Measuring the Muqarnas by al-Kashi”, Centaurus vol. 35 (1992), pp. 193-242; idem, “How al-Kashi Measures the Muqarnas: A Second Look”, in Mathematische Probleme im Mittelalter: Der lateinische und arabische Sprachbereich. Edited by Menso Folkerts (Wolfenbütteler Mittelalter-Studien, vol. 10), Wiesbaden: Harrassowitz Verlag, 1996, pp. 56-90.
[11.] On all these varieties of Muqarnas, click here to visit the survey provided by Shiro Takahashi on a large array of plans of, ordered by their geographic and historic relations.
[12.] These plans are reproduced in Ulrich Harb’s book: Ilkhanidische Stalaktitengewolbe Beitrage zu Entwurf und Bautechnik, Berlin: Dietrich Reimer Verlag, 1978.
[13.] See the Project website at Heidelberg University: Muqarnas Visualization in the Numerical Geometry Group.
[14.] Private communication on 25 February 2007.
[15.] See in particular for a first view on the work of this scholar: Branko Grünbaum, Zdenka Grünbaum, G. C. Shephard, “Symmetry in Moorish and Other Ornaments”, in Computers & Mathematics with Applications, Part B 12 (1986), no. 3-4, pp. 641-653; Branko Grünbaum, G. C. Shephard, “Interlace Patterns in Islamic and Moorish Art,” The Visual Mind, Leonardo Book Series, MIT Press, Cambridge, Mass., 1993, pp. 147-155.
[16.] Private communication on 7 March 2007.
[17.] George Saliba, “Artisans and Mathematicians in Medieval Islam”, Journal of the American Oriental Society, vol. 119 (1999), pp. 637-645. In this article, George Saliba reviews the book by Gülru Necipoglu, The Topkapi Scroll: Geometry and Ornament in Islamic Architecture. Getty’s Sketchbooks and Albums, vol. 1. Santa Monica, The Getty Center for the History of Art and the Humanities, 1995.
[18.] Alpay Özdural 1995. “Omar Khayyâm, Mathematicians and Conversazioni with Artisans” Journal of the Society of Architectural Historians vol 54: pp. 54-71 (establishes a connection between a triangle constructed by al-Khayyâm in his treatise of algebra and mosaic drawings); Alpay Özdural, “On Interlocking Similar or Corresponding Figures and Ornamental Patterns of Cubic Equations” Muqarnas (Leiden) vol. 13 (1996): pp. 191-211 (a partial analysis of an Iranian manuscript from the 13th-14th centuries including mosaic drawings that could not be drawn by compass and ruler); Alpay Özdural, “A Mathematical Sonata for Architecture: Omar Khayyam and the Friday Mosque of Isfahan.” Technology and Culture vol. 39 (1998): pp. 699-715; Alpay Özdural, “Mathematics and Arts: Connections between Theory and Practice in the Medieval Islamic World.” Historia Mathematica vol. 27 (2000): pp. 171–201
[19.] This work can be dated to around 1300 because the mathematician, Abu Bakr al-Khalil al-Tajir al-Rasadi (ca. 1300), is cited twice as one of the participants of the discussions, and the text probably came from Tabr¯iz he capital city of the Ilkhanids, which was the scene of huge construction campaigns under the sponsorship of Gazan Khan and his vizier Rashid al-Din at the turn of the fourteenth century.
[20.] Özdural, Alpay “The Use of Cubic Equations in Islamic Art and Architecture”, in Nexus IV: Architecture and Mathematics, edited by José Francisco Rodrigues and Kim Williams. Turin, Italy: Kim Williams Books, 2002. Click here to read the online abstract.
~ End ~
*Professor Salim T S Al-Hassani, Professorial Fellow, Faculty of Humanities and Arts, University of Manchester; Chairman of Foundation for Science, Technology & Civilisation, (FSTC),UK.
4.7 / 5. Votes 197
No votes so far! Be the first to rate this post.




Muslim Heritage:
Send us your e-mail address to be informed about our work.
This Website MuslimHeritage.com is owned by FSTC Ltd and managed by the Foundation for Science, Technology and Civilisation, UK (FSTCUK), a British charity number 1158509.
© Copyright FSTC Ltd 2002-2020. All Rights Reserved.
